The Birthday Paradox and Microsoft GUIDs or How I use Mathematica to Reassure Myself to Go Back to Sleep at Nights.
The Birthday Paradox
Quick, how many people must be in the same room so that the chance of at least two of them having the same birthday is 50%? 300 people?, 180 people? 100 people? The answer might surprise you. It sure did surprise me the first time I heard it.
If you have two people in the same room, the chance that they will have the same birthday is 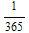 or approximately 0.003, assuming there is no such things as leap years. If you have three people in the same room, what is the chance that at least two of them have the same birthday? To find that, we notice that the chance that at least two of them having the same birthday plus the chance that all of them having distinct birthdays is one--P(at least two person have the same birthday) = 1 - P(all of them have distinct birthdays). Now the chance that all of them have distinct birthdays is
or approximately 0.003, assuming there is no such things as leap years. If you have three people in the same room, what is the chance that at least two of them have the same birthday? To find that, we notice that the chance that at least two of them having the same birthday plus the chance that all of them having distinct birthdays is one--P(at least two person have the same birthday) = 1 - P(all of them have distinct birthdays). Now the chance that all of them have distinct birthdays is 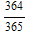 .
.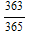 , therefore, the chance that at least two person have the same birthday is 1-
, therefore, the chance that at least two person have the same birthday is 1-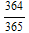 .
.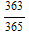 or approximately 0.008.
or approximately 0.008.
Now, if you have 365 people in the same room, you can be certain that at least two of them will have the same birthday (again assuming there is no leap year.) An interesting question is, to have a 50% chance that at least two people have the same birthday, how many people must be in the same room? The answer surprised so many people that it is called the Birthday Paradox.
First, we write down a formula for the chance that at least two people, out of k people, will have the same birthday. Let's call that p[k]. We know that p[1]=1-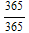 =0, p[2]=1-
=0, p[2]=1-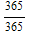
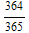 , p[3]=1-
, p[3]=1-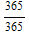
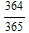
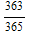 , p[4] = 1-
, p[4] = 1-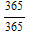
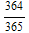
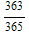
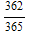 , in general: p[k] is:
, in general: p[k] is:
In[17]:=
![p[k_] := 1 - (365) !/((365 - k) ! 365^k)](HTMLFiles/birthdayparadox_16.gif)
Here are some numerical values for p[k]:
In[18]:=
![TableForm[Table[{k, N[p[k], 3]}, {k, 1, 25}], TableHeadings -> {None, {"k", "p[k] to three decimal places"}}]](HTMLFiles/birthdayparadox_17.gif)
Out[18]//TableForm=
| k |
p[k] to three decimal places |
| 1 |
0 |
| 2 |
0.00274 |
| 3 |
0.00820 |
| 4 |
0.0164 |
| 5 |
0.0271 |
| 6 |
0.0405 |
| 7 |
0.0562 |
| 8 |
0.0743 |
| 9 |
0.0946 |
| 10 |
0.117 |
| 11 |
0.141 |
| 12 |
0.167 |
| 13 |
0.194 |
| 14 |
0.223 |
| 15 |
0.253 |
| 16 |
0.284 |
| 17 |
0.315 |
| 18 |
0.347 |
| 19 |
0.379 |
| 20 |
0.411 |
| 21 |
0.444 |
| 22 |
0.476 |
| 23 |
0.507 |
| 24 |
0.538 |
| 25 |
0.569 |
Note that when we have 23 people, the chance is 50.7% that at least two of them will have the same birthday! Most people would guess that there must be a lot more than 23 people to have a 50% chance. That's why this is called the Birtday Paradox. Below is a plot of p[k] for k from 1 to 100.
In[19]:=
![Plot[p[k], {k, 1, 100}]](HTMLFiles/birthdayparadox_18.gif)
![[Graphics:HTMLFiles/birthdayparadox_19.gif]](HTMLFiles/birthdayparadox_19.gif)
Out[19]=
Microsoft GUIDs
How is the Birthday Paradox having anything to do with Microsoft GUIDs? For that matter, what is a GUID?
GUID stands for Globally Unique Identifier. It is a 128-bit number which means that if we write it down using base 2, we will need 128 digits of either one or zero to represent it. If we write it down in our usual base 10, we will need about 38 digits (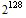 ~ 3.4 x
~ 3.4 x 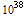 .)
.)
Under Microsoft Windows, it's more and more likely that most of the programs, package routines, and other programming components will be labeled with GUIDs. To make everything works, each GUID must be truely unique. Microsoft Windows relies on the fact that every distinct object has its own distinct GUID label. If a GUID is repeated, unpredictable behaviors will occur. Definitely a bad thing. So, the question is, how can we be sure that the GUIDs never repeat?
The answer to that question is that we can never be sure. The only thing that prevents GUIDs from repeating is the fact that the number of values that GUIDs can be is enormous. There can be the total of 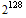 (or 3.4 x
(or 3.4 x 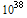 ) distinct GUIDs. Microsoft provides us with a CoCreateGuid function to generate "extremely likely distinct" GUIDs. If the function works as advertised, how many GUIDs must be generate before there is an appreciable chance that they start to repeat? That's the question that occured to me when I had to generate quite a number of GUIDs for my programming projects.
) distinct GUIDs. Microsoft provides us with a CoCreateGuid function to generate "extremely likely distinct" GUIDs. If the function works as advertised, how many GUIDs must be generate before there is an appreciable chance that they start to repeat? That's the question that occured to me when I had to generate quite a number of GUIDs for my programming projects.
The first thing that we should notice is that this problem is the same problem as the Birthday Paradox problem, with the number of days in a year equals to 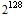 instead of 365, the people in a room are replaced by GUIDs, and the question becomes "How many GUIDS must be generated before at least two of them repeat?"
instead of 365, the people in a room are replaced by GUIDs, and the question becomes "How many GUIDS must be generated before at least two of them repeat?"
We replace the formula for p[k] with p[N,k] where p[N,k] is the chance of having at least two GUIDs with the same value, given that the number of possible GUIDs is N. We just replace 365 in p[k] with N and get our new formula:
In[29]:=
![p[N_, k_] := 1 - (N) !/((N - k) ! N^k)](HTMLFiles/birthdayparadox_26.gif)
To check our new formula, we calculate p[365,23]:
In[31]:=
![p[365, 23]//N](HTMLFiles/birthdayparadox_27.gif)
Out[31]=
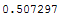
This agree with p[23].
Since we will deal with extremely large N, it's a good idea to find some approximation so that the factorials will not exhaust our computing resource. We use the first term of Stirling approximation of factorial function:
In[22]:=
![Normal[Series[Factorial[x], {x, Infinity, 1}]]](HTMLFiles/birthdayparadox_29.gif)
Out[22]=
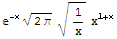
and define logfactorial function to be the natural log of the approximation:
In[23]:=
![logfactorial[x_] := x Log[x] - x + 1/2Log[2 Pi x]](HTMLFiles/birthdayparadox_31.gif)
To see how good our approximation is, we list some of its relative errors:
In[32]:=
![RowBox[{TableForm, [, RowBox[{RowBox[{Table, [, RowBox[{RowBox[{{, RowBox[{2^x, ,, RowBox[{100 ... ]}], ,, TableHeadings -> {None, {"n", "% error of approximated n!"}}}], ]}]](HTMLFiles/birthdayparadox_32.gif)
Out[32]//TableForm=
| n |
% error of approximated n! |
| 8 |
-1.03573 |
| 16 |
-0.519412 |
| 32 |
-0.260069 |
| 64 |
-0.130123 |
| 128 |
-0.0650828 |
| 256 |
-0.0325468 |
| 512 |
-0.0162747 |
| 1024 |
-0.00813769 |
So, for n as small as 8, our approximate n! is off by only a percent. We then write an approximate formula for p[N,k] for large N, replacing all the factorials with its Stirling approximation:
In[33]:=
![approxP[N_, k_] := 1 - Exp[ -k Log[N] + ((N) Log[N] - (N) + 1/2Log[2Pi (N)]) - ((N - k) Log[N - k] - (N - k) + 1/2Log[2Pi (N - k)])]](HTMLFiles/birthdayparadox_33.gif)
In[35]:=
![approxP[365, 23]//N](HTMLFiles/birthdayparadox_34.gif)
Out[35]=
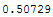
Now, we notice that at large N, p[N, k] will be appreciable only for k at least as large as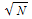 , so we try to find a limit for p[N, a
, so we try to find a limit for p[N, a 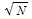 ] for positive number a:
] for positive number a:
In[36]:=
![Limit[approxP[N, a N^(1/2)], {N->Infinity}]](HTMLFiles/birthdayparadox_38.gif)
Out[36]=
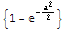
We then try to find a value of a for which p[N, a 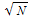 ] is equal to 0.5:
] is equal to 0.5:
In[37]:=
![RowBox[{Solve, [, RowBox[{RowBox[{1 - E^(-a^2/2), ==, , 0.5}], ,, a}], ]}]](HTMLFiles/birthdayparadox_41.gif)
Out[37]=
![RowBox[{{, RowBox[{RowBox[{{, RowBox[{a, , RowBox[{-, 1.17741}]}], }}], ,, RowBox[{{, RowBox[{a, , 1.17741}], }}]}], }}]](HTMLFiles/birthdayparadox_43.gif)
Therefore, p[N,1.18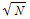 ] is about 0.5 for large N. This means that if the total number of distinct GUIDs is N, we can expect to generate about 1.18
] is about 0.5 for large N. This means that if the total number of distinct GUIDs is N, we can expect to generate about 1.18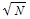 GUIDs before there is a 50% chance that they repeat. In our case, N is
GUIDs before there is a 50% chance that they repeat. In our case, N is 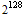 and 1.18
and 1.18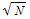 is about 2 x
is about 2 x 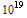 which is definitely a big number.
which is definitely a big number.
Let's say that there are a million programmers each generating a million GUIDs per seconds, it will take 2 x 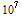 seconds or 116 days to generate 2 x
seconds or 116 days to generate 2 x 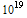 GUIDs. A more likely situation is 100,000 programmers each generating 1 GUID per hour. This will take 2 x
GUIDs. A more likely situation is 100,000 programmers each generating 1 GUID per hour. This will take 2 x 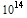 hours or twenty two billion years to generate 2 x
hours or twenty two billion years to generate 2 x 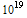 GUIDs. For those of you who still wonder, our estimated age of the universe since big bang is between 12 and 15 billion years.
GUIDs. For those of you who still wonder, our estimated age of the universe since big bang is between 12 and 15 billion years.
So, assuming that the implementation of the GUID genenating function is not defective, I don't think I will generate repeating GUIDs anytime soon. However, considering how buggy Microsoft Windows can be, it wouldn't surprise me that there will be a crisis arising from repeating GUIDs akin to our current Year-2000 problems before I die :-)
Created by
Mathematica
(July 7, 2004)
![[Graphics:HTMLFiles/birthdayparadox_19.gif]](HTMLFiles/birthdayparadox_19.gif)